条件随机场模型简介

本文是对条件随机场的简单介绍，主要基于 Conditional Random Fields: An Introduction [pdf] 这篇文章，作者是 Hanna M. Wallach。

为什么用 CRF 做序列标注

HMM 定义联合概率分布 $p(X, Y)$，其中 $X, Y$ 取遍所有观测序列和相应的标签序列。假定任意时刻的观测结果只和该时刻的状态（标签）相关，忽略多元关系和长程关系。

一个解决办法是避免对全体 $X$ 建模，只对特定的观测序列 $x$ 进行标注。引入条件概率 $p(Y \mid x)$，对它进行标注就是求 $y^{\star} = \mathrm{argmax}_y p(y \mid x)$。 显然，这意味着 CRF 不是一个生成模型，而是判别模型。

它的优点是：条件概率放松了 HMM 的独立性假定；全局归一化避免了 MEMM 的 label bias 问题。

CRF 的无向图模型

给定一个观测序列，定义在标签序列上的 log-linear 分布。

在无向图 $G = (V,E)$ 上，每个 $v \in V$ 对应一个标签，且满足马尔可夫性质。 利用图结构，将 $Y_v$ 的联合概率分布分解为势函数的乘积（并经过归一化）。

在序列（即线性链）中，马尔可夫性质是指每个 $Y_i$ 只与 $Y_{i-1}$ 有关，与其他的 $Y_j$ 都无关。于是，势函数只依赖相邻的标签变量 $Y_i$ 和 $Y_{i-1}$。

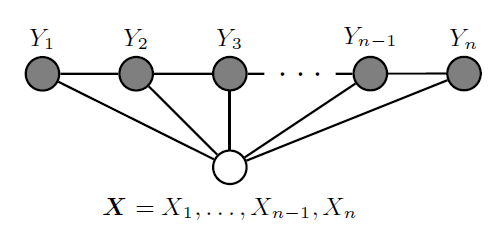
CRF 条件随机场

令 $\lambda$ 表示待估计的参数，

其中 $Z(x)$ 是归一化因子； $F_j(y, x) = \sum_i f_j(y_{i-1}, y_i, x, i)$ ，每个 $f_j$ 可以是状态特征函数 $s(y_i, x, i)$ 或者转移特征函数 $t(y_{i-1}, y_i, x, i)$，通常是取值为0或1的示性函数，表示某个特征是否出现。

例如，可以定义 $t(y_{i-1},y_i,x,i)$ 在 $y_{i-1}=\mbox{IN}$ 且 $y_i=\mbox{NNP}$ 且 $x_i=\mbox{‘September’}$ 时取值为1，否则取值为0。

最大熵

从有限的训练数据估计概率分布，最大熵原则：从不完全信息中得出的概率分布应当使熵最大化（在服从给定的约束的前提下）。

在这里，给定的约束就是：每个特征函数在模型分布上的期望应当等于在数据上观测到的期望。

参数的最大似然估计

对于训练数据 ${(x^{(k)}, y^{(k)})}$，假定它们独立同分布，似然（likelihood）等于 $p(\{y^{(k)}\} \mid \{x^{(k)}\}, \lambda) = \prod_k p(y^{(k)}\mid x^{(k)}, \lambda) = \prod_k \frac{1}{Z(x^{(k)})} \exp{\bigl( \sum_j \lambda_j F_j(y^{(k)}, x^{(k)}) \bigr)}$

取对数，得到 对数似然 $\mathcal{L} (\lambda) = \sum_k \log p(y^{(k)} \mid x^{(k)}, \lambda) = \sum_k \Bigl[ \log \frac{1}{Z(x^{(k)})} + {\sum_j \lambda_j F_j(y^{(k)}, x^{(k)})} \Bigr]$

对参数分量求微分， $\frac{\partial \mathcal{L} (\lambda)}{\partial \lambda_j} = E_{\tilde{p}(Y, X)} [F_j (Y, X)] - \sum_k E_{p(Y \mid x^{(k)}, \lambda)} [F_j (Y, x^{(k)})]$

其中 $\tilde{p}(Y, X)$ 是观测分布，$E_p[f]$ 是 $f$ 在分布 $p$ 上的期望。令上式为 0 就得到最大熵模型约束。

这个优化问题没有分析解，可以通过迭代的方法求近似解。

矩阵计算

给定观测序列，计算标签序列的概率时，我们希望计算归一化因子 $Z$，可以利用矩阵提高计算效率，具体过程此处从略。

动态规划

在估计参数时，我们希望对每个观测序列计算各个特征函数的期望，可以利用动态规划，类似于 HMM 的前向后向算法，具体过程此处从略。