卷积神经网络运算扫盲

卷积神经网络（CNN）非常重要，但是缺乏信号处理背景的初学者多半会感到难以准确理解其细节。本文目的就在于解释清楚卷积（包括池化、反卷积）的各参数的作用，具体的计算方式，以及究竟什么是反卷积。本文假设读者了解矩阵乘法，对神经网络有基本的认识。

本文主要参考文献及动图来源：

Vincent Dumoulin, Francesco Visin. A guide to convolution arithmetic for deep learning. (arXiv, GitHub)
How do I derive the back propagation algorithm in Convolutional Neural Network? (Quora)

其他参考文献及推荐阅读：

Goodfellow et al. Deep Learning. (在线阅读)

卷积

卷积层的输入、输出是多维数组，称为 feature map；卷积操作的核心组件也是多维数组，称为 kernel 或 filter。每次 kernel 在输入的 feature map 上面滑动一步，覆盖住它的一部分，两个数组对应位置上的元素分别相乘，最后求和，就得到输出的一个元素。kernel 在输入的 feature map 上完整地滑动一遍，就得到完整的输出。

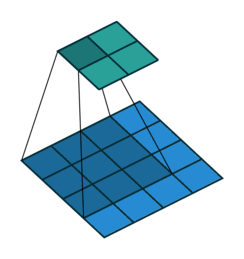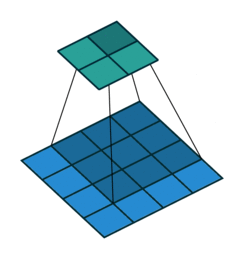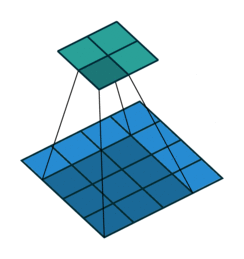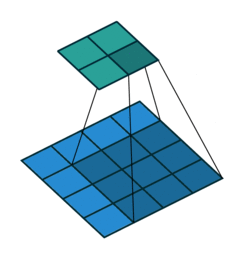
可见，离散卷积有两个特点。一是稀疏，每个输出元素计算时只用到少数几个输入元素的数值，即感受野（receptive field）比较小；相比之下，全连接层每个神经元的感受野都是全体输入。二是共享参数，不同位置都是用相同的 kernel 计算的。

如果 kernel 是二维数组，这就是一个二维卷积；也可以推广到 N 维卷积，此时 kernel 就是 N 维数组。如果输入是多个 feature map，也需要 kernel 相应增加一个维度。

卷积的参数和输出形状

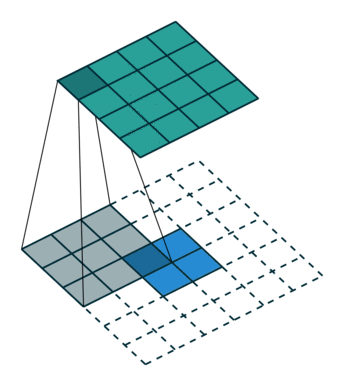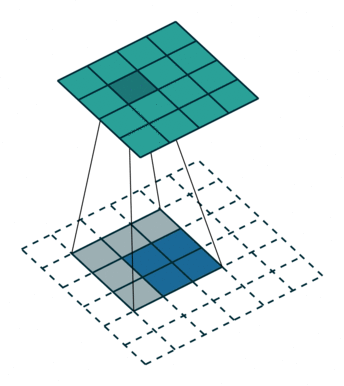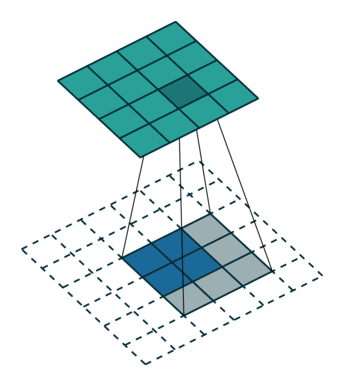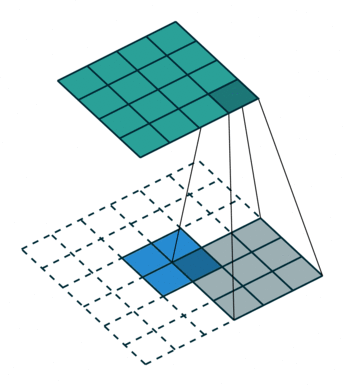
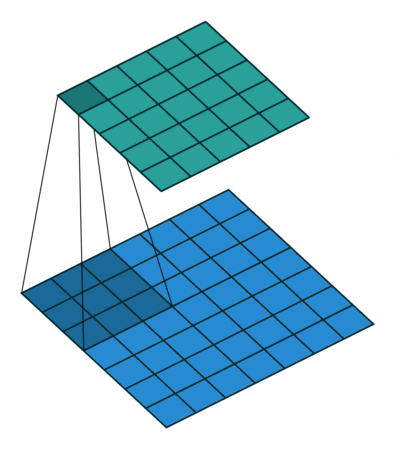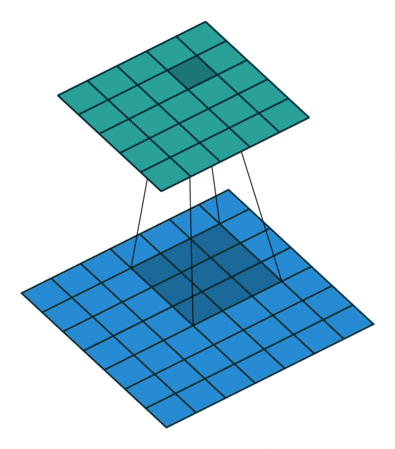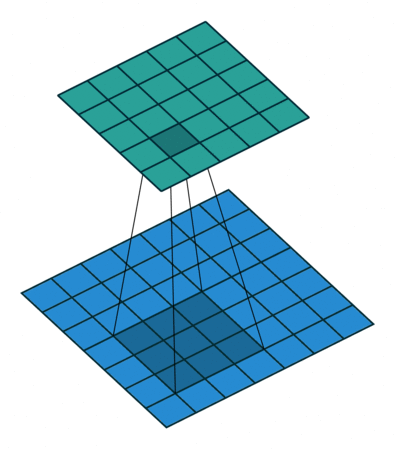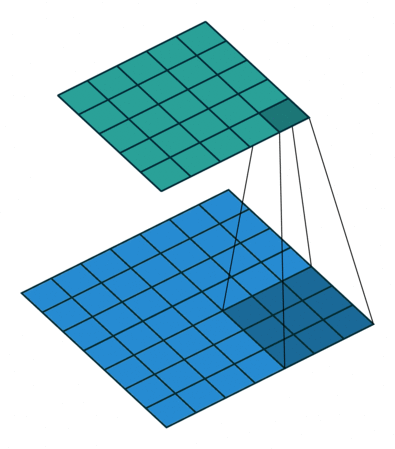
为方便演示，下面针对二维卷积推导输出数组的形状。我们采用一种非常简化的假设：输入为 $i \times i$ 数组，kernel 为 $k \times k$ 数组，两个维度的步长 $s$ 相同，每一边外侧补零的个数 $p$ 也相同。

首先看单位步长（$s = 1$）的情形：

不补零（no padding），$p = 0$，观察可知 $o = (i - k) + 1$
补零（zero padding），观察可知 $o = (i - k) + 2p + 1$；有两种常见的补零方式：
- 半补零，使得输出与输入大小相同（same padding），此时有 $k = 2p + 1$，于是 k 应当是奇数，$p = \lfloor{\frac{k}{2}}\rfloor$（因此也称为 half padding）
- 全补零，使得 feature map 与 kernel 的所有重叠都被取到（full padding），于是 $p = k - 1$，推出 $o = i + (k - 1)$

然后是 $s > 1$

不补零，$p = 0$，观察可知 $o = \lfloor{\frac{i-k}{s}}\rfloor + 1$
补零，类似有 $o = \lfloor{\frac{i+2p-k}{s}}\rfloor + 1$

注意到取整函数的存在，不同大小的输入可能产生相同大小的输出。这一点在反卷积的时候会用到。


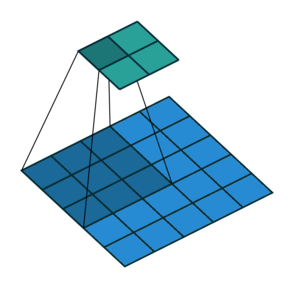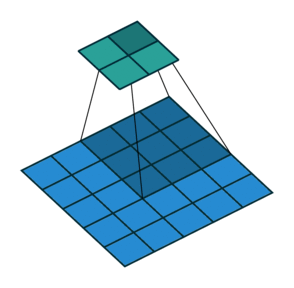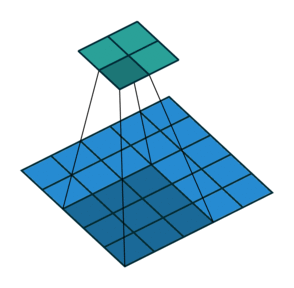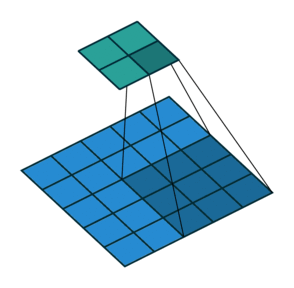
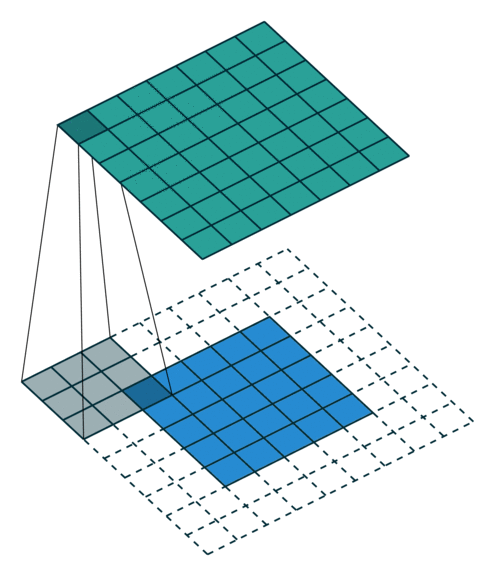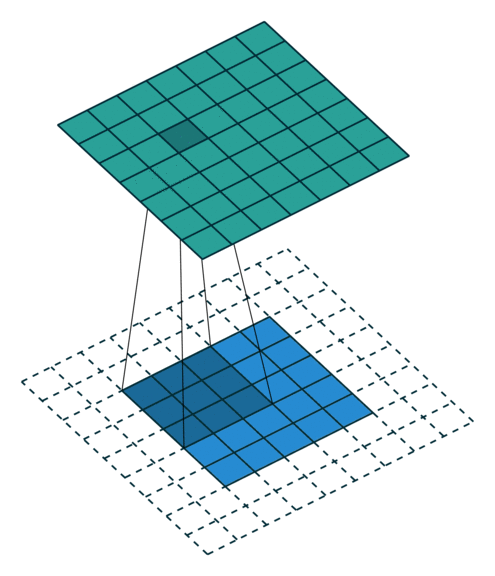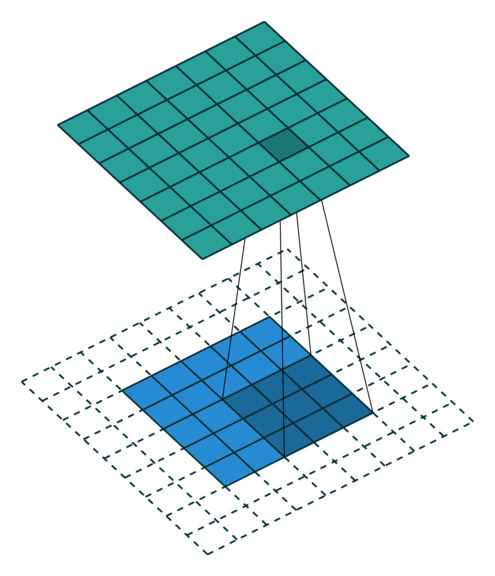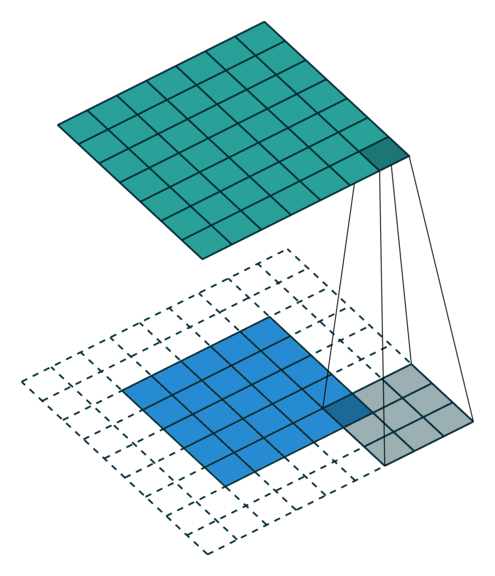
卷积，不补零，步长为 1	卷积，不补零，步长为 2	卷积，全补零，步长为 1

卷积的矩阵运算

考虑二维卷积，$p = 0$，$ s = 1$。

设 kernel 为 $3 \times 3$ 数组

$W = \begin{pmatrix} w_{0,0} & w_{0,1} & w_{0,2} \\ w_{1,0} & w_{1,1} & w_{1,2} \\ w_{2,0} & w_{2,1} & w_{2,2} \end{pmatrix}$

输入 feature map 为 $4 \times 4$ 的数组

$X = \begin{pmatrix} x_{0,0} & x_{0,1} & x_{0,2} & x_{0,3}\\ x_{1,0} & x_{1,1} & x_{1,2} & x_{1,3}\\ x_{2,0} & x_{2,1} & x_{2,2} & x_{2,3}\\ x_{3,0} & x_{3,1} & x_{3,2} & x_{3,3} \end{pmatrix}$

将输入展平为一维列向量

$X_{flat} = (x_{0, 0}, x_{0, 1}, x_{0, 2}, x_{0, 3}, x_{1, 0}, \cdots, x_{3,3})^T$

记卷积结果为 $Y$ 并按照相同顺序展平为一维向量，根据卷积定义可以直接写出

$Y_{flat} = \begin{pmatrix} w_{0,0}x_{0,0} + w_{0,1}x_{0,1} + w_{0,2}x_{0,2} + w_{1,0}x_{1,0} + w_{1,1}x_{1,1} + w_{1,2}x_{1,2} + w_{2,0}x_{2,0} + w_{2,1}x_{2,1} + w_{2,2}x_{2,2} \\ w_{0,0}x_{0,1} + w_{0,1}x_{0,2} + w_{0,2}x_{0,3} + w_{1,0}x_{1,1} + w_{1,1}x_{1,2} + w_{1,2}x_{1,3} + w_{2,0}x_{2,1} + w_{2,1}x_{2,2} + w_{2,2}x_{2,3} \\ w_{0,0}x_{1,0} + w_{0,1}x_{1,1} + w_{0,2}x_{1,2} + w_{1,0}x_{2,0} + w_{1,1}x_{2,1} + w_{1,2}x_{2,2} + w_{2,0}x_{3,0} + w_{2,1}x_{3,1} + w_{2,2}x_{3,2} \\ w_{0,0}x_{1,1} + w_{0,1}x_{1,2} + w_{0,2}x_{1,3} + w_{1,0}x_{2,1} + w_{1,1}x_{2,2} + w_{1,2}x_{2,3} + w_{2,0}x_{3,1} + w_{2,1}x_{3,2} + w_{2,2}x_{3,3} \\ \end{pmatrix}$

显然这是两个矩阵的乘积，即 $ Y_{flat} = C X_{flat}$，其中

$C = \begin{pmatrix} w_{0,0} & w_{0,1} & w_{0,2} & 0 & w_{1,0} & w_{1,1} & w_{1,2} & 0 & w_{2,0} & w_{2,1} & w_{2,2} & 0 & 0 & 0 & 0 & 0 \\ 0 & w_{0,0} & w_{0,1} & w_{0,2} & 0 & w_{1,0} & w_{1,1} & w_{1,2} & 0 & w_{2,0} & w_{2,1} & w_{2,2} & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & w_{0,0} & w_{0,1} & w_{0,2} & 0 & w_{1,0} & w_{1,1} & w_{1,2} & 0 & w_{2,0} & w_{2,1} & w_{2,2} & 0 \\ 0 & 0 & 0 & 0 & 0 & w_{0,0} & w_{0,1} & w_{0,2} & 0 & w_{1,0} & w_{1,1} & w_{1,2} & 0 & w_{2,0} & w_{2,1} & w_{2,2} \end{pmatrix}$

于是我们将卷积转化为矩阵计算。特别指出，这个矩阵是一个循环矩阵的变体。对于其他情形，也可以写出类似的表示。

上述计算方法相当于将 kernel 按照输入形状展开。由于实践中往往是输入尺寸远大于 kernel 尺寸，因此反过来将输入按照 kernel 形状展开更为高效。确切说来，首先将 kernel 展平为行向量，再将输入的 feature map 按照滑动窗口顺序展开为若干列向量，第一列对应第一个滑动窗口，第二列对应第二个滑动窗口，以此类推。这样，上面的例子就转化为一个并不复杂、可以并行计算的矩阵乘法

$Y_{flat}^T = \begin{pmatrix} w_{0,0} & w_{0,1} & w_{0,2} & w_{1,0} & w_{1,1} & w_{1,2} & w_{2,0} & w_{2,1} & w_{2,2} \end{pmatrix} \cdot \begin{pmatrix} x_{0,0} & x_{0,1} & x_{1,0} & x_{1,1} \\ x_{0,1} & x_{0,2} & x_{1,1} & x_{1,2} \\ x_{0,2} & x_{0,3} & x_{1,2} & x_{1,3} \\ x_{1,0} & x_{1,1} & x_{2,0} & x_{2,1} \\ x_{1,1} & x_{1,2} & x_{2,1} & x_{2,2} \\ x_{1,2} & x_{1,3} & x_{2,2} & x_{2,3} \\ x_{2,0} & x_{2,1} & x_{3,0} & x_{3,1} \\ x_{2,1} & x_{2,2} & x_{3,1} & x_{3,2} \\ x_{2,2} & x_{2,3} & x_{3,2} & x_{3,3} \end{pmatrix}$

卷积的梯度计算

定义函数 conv2d(input, kernel, pad, stride)。沿用前面的记号，有

$Y = \mathrm{conv2d}(\mathrm{input}=X, \mathrm{kernel}=W, \mathrm{pad}=0, \mathrm{stride}=1)$

其中 $X$、$W$、$Y$ 分别为 $4 \times 4$、$3\times 3$、$2 \times 2$ 矩阵。

设 $J$ 为损失函数，下面求梯度 $\frac{\partial J}{\partial W}$ 和 $\frac{\partial J}{\partial X}$。

$\frac{\partial J}{\partial w_{00}} = \sum_{i,j} \frac{\partial J}{\partial y_{ij}} \frac{\partial y_{ij}}{\partial w_{00}} = \frac{\partial J}{\partial y_{00}} x_{00} + \frac{\partial J}{\partial y_{01}} x_{01} + \frac{\partial J}{\partial y_{10}} x_{10} + \frac{\partial J}{\partial y_{11}} x_{11}$

同样可以求出

$\frac{\partial J}{\partial w_{01}} = \frac{\partial J}{\partial y_{00}} x_{01} + \frac{\partial J}{\partial y_{01}} x_{02} + \frac{\partial J}{\partial y_{10}} x_{11} + \frac{\partial J}{\partial y_{11}} x_{12}$ $\frac{\partial J}{\partial w_{02}} = \frac{\partial J}{\partial y_{00}} x_{02} + \frac{\partial J}{\partial y_{01}} x_{03} + \frac{\partial J}{\partial y_{10}} x_{11} + \frac{\partial J}{\partial y_{11}} x_{13}$ $\frac{\partial J}{\partial w_{10}} = \frac{\partial J}{\partial y_{00}} x_{10} + \frac{\partial J}{\partial y_{01}} x_{11} + \frac{\partial J}{\partial y_{10}} x_{20} + \frac{\partial J}{\partial y_{11}} x_{21}$

以下省略。将它们代入

$\frac{\partial J}{\partial W} = \begin{pmatrix} \frac{\partial J}{\partial w_{00}} & \frac{\partial J}{\partial w_{10}} & \frac{\partial J}{\partial w_{20}}\\ \frac{\partial J}{\partial w_{01}} & \frac{\partial J}{\partial w_{11}} & \frac{\partial J}{\partial w_{21}}\\ \frac{\partial J}{\partial w_{02}} & \frac{\partial J}{\partial w_{12}} & \frac{\partial J}{\partial w_{22}} \end{pmatrix}$

容易看出实际上就是

$\frac{\partial J}{\partial W} = \mathrm{conv2d}( \mathrm{input} = \begin{pmatrix} x_{0,0} & x_{0,1} & x_{0,2} & x_{0,3}\\ x_{1,0} & x_{1,1} & x_{1,2} & x_{1,3}\\ x_{2,0} & x_{2,1} & x_{2,2} & x_{2,3}\\ x_{3,0} & x_{3,1} & x_{3,2} & x_{3,3} \end{pmatrix}, \mathrm{kernel}= \begin{pmatrix} \frac{\partial J}{\partial y_{00}} & \frac{\partial J}{\partial y_{10}} \\ \frac{\partial J}{\partial y_{01}} & \frac{\partial J}{\partial y_{11}} \end{pmatrix}, \mathrm{pad}=0, \mathrm{stride}=1)$

即

$\frac{\partial J}{\partial W} = \mathrm{conv2d}(\mathrm{input} = X, \mathrm{kernel}=\frac{\partial J}{\partial Y}, \mathrm{pad}=0, \mathrm{stride}=1)$

这里的 gradient matrix 采用了 numerator layout 的记法。关于矩阵求导及其 numerator layout，见前一篇文章。

再对 $X$ 的每个元素类似计算，可得

$\frac{\partial J}{\partial X} = \mathrm{conv2d}( \mathrm{input}= \begin{pmatrix} \frac{\partial J}{\partial y_{00}} & \frac{\partial J}{\partial y_{10}} \\ \frac{\partial J}{\partial y_{01}} & \frac{\partial J}{\partial y_{11}} \end{pmatrix}, \mathrm{kernel}= \begin{pmatrix} w_{2,2} & w_{2,1} & w_{2,0}\\ w_{1,2} & w_{1,1} & w_{1,0}\\ w_{0,2} & w_{0,1} & w_{0,0} \end{pmatrix}, \mathrm{pad}=\mathrm{full}, \mathrm{stride}=1)$

即

$\frac{\partial J}{\partial X} = \mathrm{conv2d}(\mathrm{input}=\frac{\partial J}{\partial W}, \mathrm{kernel}=W_{reverse}, \mathrm{pad}=\mathrm{full}, \mathrm{stride}=1)$

其中 $W_{reverse}$ 是将 $W$ 旋转 180 度，或者说是将 $W$ 的各行、各列元素逆序。

不难理解为什么要将 $W$ 的元素逆序排列。在计算卷积的时候，除了边缘以外， $Y$ 中的每个元素 $y_{i,j}$ 都受到 $X$ 的 $3 \times 3$ 个元素的影响，即 $x_{i’,j’}$，其中 $\lvert{i’-i}\rvert \leq 1, \lvert{j’-j}\rvert \leq 1$；这正是由卷积 kernel 定义的感受野。

反过来思考，$X$ 中的每个元素 $x_{i,j}$ 也一样影响 $Y$ 中的 $3 \times 3$ 区域的元素，即 $y_{i’,j’} $，其中 $\lvert{i’-i}\rvert \leq 1, \lvert{j’-j}\rvert \leq 1$。既然 kernel 是从左到右、从上到下地滑过 $X$，也就是说 $X$ 中的每一元素是从右到左、从下到上地与 kernel 中的元素相结合。因此计算 $\frac{\partial J}{\partial X}$ 时，会用到 $W_{reverse}$。

由上面的推导可见，卷积的反向传播函数也是卷积操作。

池化

池化（pooling）与卷积操作类似，也是一个窗口在 feature map 上面滑动，每到一处将当前覆盖的所有元素整合为一个元素。这是一个下采样过程，常见的整合步骤包括取出当前区域的最大值（max pooling）、平均值（average pooling）等等。

Springenber et al. (2015) 已经推导过，池化相当于对特征进行卷积，激活函数是 $p$ 范数。当 $ p \rightarrow \infty$ 时，就得到 max pooling。因此他们尝试构建了一个完全由卷积层构成的模型，有兴趣可以阅读原文。

与卷积类似，可以推导出 $o = \lfloor{\frac{i-k}{s}}\rfloor + 1$。

池化的翻译过于字面，pool 在这里其实是聚拢、集中的意思，例如下面两个例句：

We pooled ideas and information. 我们集思广益，共享信息。（柯林斯词典）

Police forces across the country are pooling resources in order to solve this crime. 全国各地警方通力合作以侦破这宗罪案。（牛津词典）

反卷积

有时候我们想要逆转编码的过程，把低维的 feature map 投射到高维空间。比如一个自编码器，我们自然希望用一种类似于编码器逆操作的模型作为解码器。

如果输入 $X$ 经过卷积操作输出 $Y$，反卷积（deconvolution）就是由 $Y$ 恢复出 $X$ 的形状的操作。我们强调，该操作只是重建了 $X$ 的空间，并不能保证恢复出 $X$ 的内容本身，因而反卷积并不是卷积的逆运算，严格讲这个术语具有误导性，但是因其在文献中十分常见，这里我们还是沿用它。

仍然使用之前的例子，考虑 $3 \times 3$ 的二维卷积 kernel， $4 \times 4$ 的二维输入 feature map，$p=0$，$s=1$。我们已经推导过，输出的形状是 $2 \times 2$。

此时如果再施加另一个 $3 \times 3$ 的二维卷积 kernel，$p’ = 2$，$s’=1$，就可以恢复成 $4 \times 4$ 的 feature map。也就是说，第一，反卷积可以用卷积来实现；第二，反卷积和卷积可以采用相同形状的 kernel，通过调节 $p$ 和 $s$ 来调节输入输出的形状关系。

反卷积的参数和输出形状

直观理解，我们通过调节补零个数，使反卷积、卷积的输入输出的边角保持大致的对应关系。例如，如果卷积没有对输入补零，输出的左上角元素就对应输入的左上区域；那么反卷积就应恰恰相反，输出的左上区域对应输入的左上角元素，因此反卷积应当进行 full padding。类似地，可以推导出不同情形的反卷积的参数和输出形状。

首先看单位步长（$s = 1$）的情形：

卷积不补零，$p = 0$，对应反卷积有 $s’ = s$，$p’=k-1$，$o’ = i’ + (k -1)$
卷积补零，对应反卷积有 $s’=s$，$p’=k-p-1$， $o’ = i’ + (k-1) - 2p$
- 卷积 same padding，此时有 $k = 2p + 1$，对应反卷积有 $s’=s$，$p’=p$，$o’=i’$
- 卷积 full padding，此时有 $p = k - 1$，对应反卷积有 $s’=s$，$p’=0$，$o’=i’- (k-1)$

然后是 $s > 1$ 的情形，直觉上我们会想到反卷积应当有 $ s < 1$，也就是说不光对反卷积的输入外部补零，还可以在内部用棋盘格的形式填充零，或者采取其他的平滑方式：

卷积不补零，$p = 0$，$i-k$ 是 $s$ 的整数倍，对应反卷积有 $s’=1$，$p’=k-1$，$o’=s(i’-1)+k$
卷积补零，$i+2p-k$ 是 $s$ 的整数倍，对应反卷积有 $s’=1$，$p’=k-p-1$，$o’=s(i’-1)+k-2p$

不是整数倍的情况下，也可以进行反卷积，只是此时补零不对称而已。

卷积	反卷积

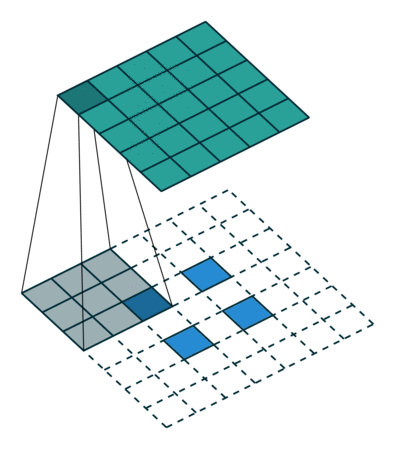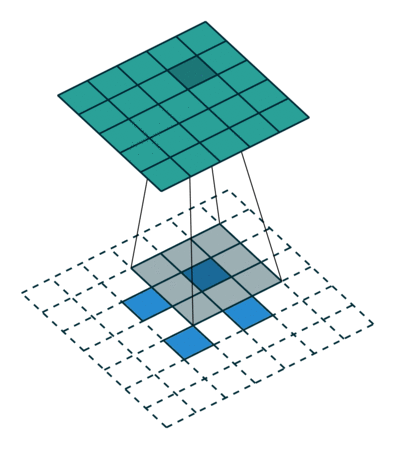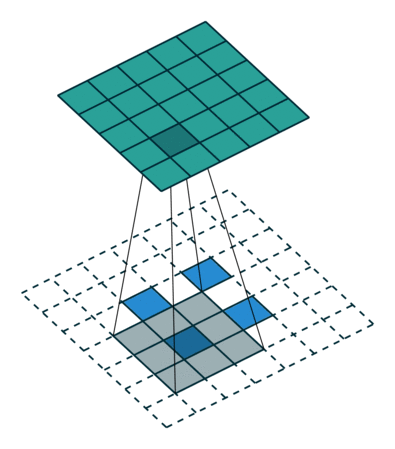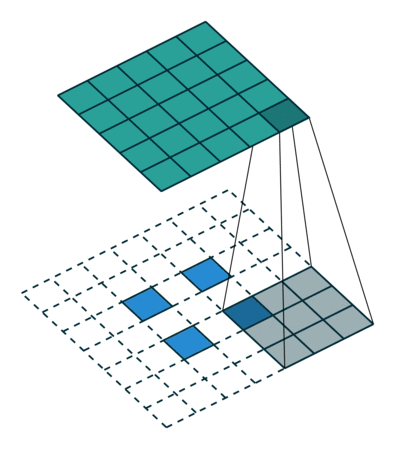
在反转池化层操作的时候，常见的方式也是补零——在正向计算 max pooling 的时候，同时记录每个区域内最大值所在的位置，从而在反向计算时可以直接将它放入相应位置，其余位置补零。

反卷积用于可视化

在论文 Visualizing and Understanding Convolutional Networks (Zeiler & Fergus, 2013) 中，作者提出可以用反卷积层对卷积神经网络进行可视化。实际上，这里的反卷积没有引入额外的参数，只是相当于原有卷积网络的反向传播过程。

论文全文见 arXiv。

前面已经推导过，卷积的反向传播也是卷积；原始 kernel 旋转 180 度就是反向传播中的 kernel，因而反卷积也被称为转置卷积（transposed convolution）。再次强调，这里所谓的反卷积并不是卷积的逆运算。

设第 $k$ 个卷积层的 kernel 为 $W^{(k)}$，输入数组为 $X^{(k-1)}$，卷积输出数组为 $Y^{(k)}$，经过池化和激活函数之后的数组为 $X^{(k)}$，即下一层的输入。那么有

$Y^{(k)} = \mathrm{conv2d}(X^{(k-1)}, W^{(k)})$ $\frac{\partial J}{\partial X^{(k)}} = \mathrm{conv2d}(\frac{\partial J}{\partial Y^{(k)}}, W_{\mathrm{reverse}}^{(k)})$

因而相应的反卷积层的 kernel 为 $W_{\mathrm{reverse}}^{(k)}$，反卷积的输入为 $\frac{\partial J}{\partial Y^{(k)}}$，输出为 $\frac{\partial J}{\partial X^{(k)}}$。因此，这个反卷积层结构能够展示出损失函数对各层输入的导数，即每一层的每一个 kernel 分别是被哪些输入信号激活了，识别出了哪些特征，从而对卷积神经网络的建模能力进行可视化。

Previous Next

sighsmile / 2018-07-29
Published under (CC) BY-NC-SA